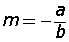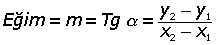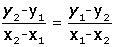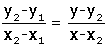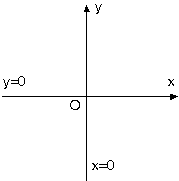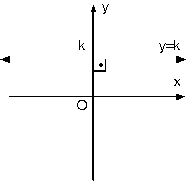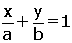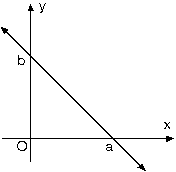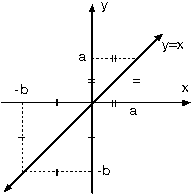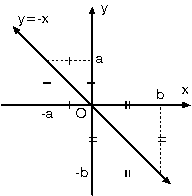YGS-LYS, Konu Anlatımı
Doğrunun Analitik İncelemesi
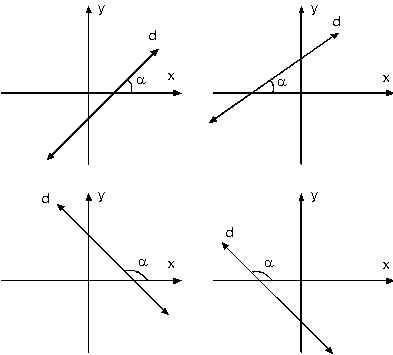
Bir doğru üzerindeki noktaların koordinatlarını veren eşitliğe doğrunun denklemi denir.
y = mx + n eşitliğinde m: eğim, n: sabit sayıdır. ax + by + c = 0 şeklinde verilen denklemde y yalnız bırakılırsa
x in katsayısı Öyle ise, ax + by + c = 0 doğrusunun eğimi
Eğimi eşit olan doğrulara paralel doğrular denir. Doğruların eğimleri arasındaki bağıntıdan daha sonra bahsedeceğiz. 2. İki Noktası Bilinen Doğrunun Eğim ve Denklemi a. İki noktası bilinen doğrunun eğimi
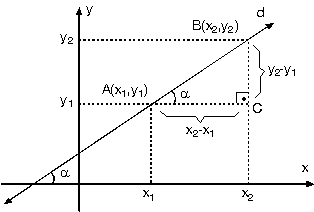
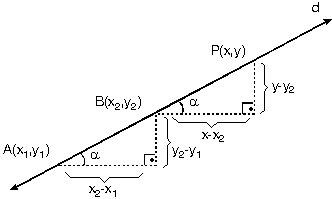
Analitik düzlemde A(x1, y1), B(x2, y2) noktaları bilinen d doğrusu üzerinde A, B noktalarının koordinatları kullanılarak oluşturulan ABC üçgeninin A açısı ile d doğrusunun eğim açısı yöndeş açılar olduklarından eşittirler. Buradan
b. İki noktası bilinen doğrunun denklemi
A(x1, y1), B(x2, y2) noktalarından geçen d doğrusu üzerinde doğruyu oluşturan noktaları temsil eden P(x, y) noktası alalım. Bu üç noktadan herhangi ikisini kullanarak yazacağımız eğimler eşittir. Buna göre,
Bu eşitlik bize iki noktası bilinen doğru denklemini verir.
şeklinde de yazılabilir. Sonuç aynıdır.
y = mx + n denklemindeki n terimi sıfır olur. O halde orijinden geçen doğrunun eğimi m ise denklemi
Doğru denklemi ax + by + c = 0 şeklinde ise ve orijinden geçiyorsa c = 0 dır. Doğru denklemi ax + by = 0 olur. 3. Bir Noktası ve Eğimi Bilinen Doğrunun Denklemi
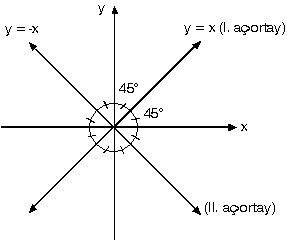
A(x1, y1) noktası ve P(x, y) noktası kullanılarak yazılan eğim değeri verilen eğime eşitlenir. 4. Eksenlere Paralel Doğruların Denklemi a. Eksen doğruları
b. x eksenine paralel doğrular
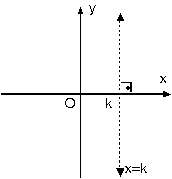
c. y eksenine paralel doğrular
5. Eksenleri Kestiği Noktaları Bilinen Doğruların Denklemi
Doğru (a, 0) ve (0, b) noktalarından geçtiğine göre, doğrunun denklemi iki noktadan geçen doğru denklemi özelliği kullanılarak da yazılabilir.
6. Doğruların Grafikleri Doğruların grafiklerini çizmek için x ve y eksenlerini kestikleri noktalar bulunur. x eksenini kestiği nokta için y = 0 ve y eksenini kestiği nokta için x = 0 değerleri alınır. |



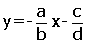
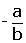 eğimi verir.
eğimi verir.