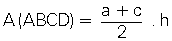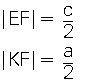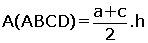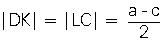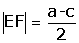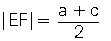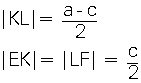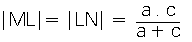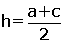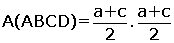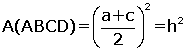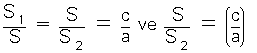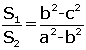Yamuk
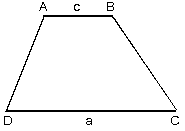
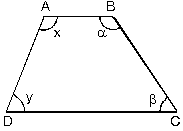
| Alt ve üst kenarları paralel olan dörtgenlere yamuk denir.Şekildeki ABCD yamuğunda [AB] // [DC] dir. |
 |
1. Yamukta açılar
| [AB] // [DC] olduğundan
|
 |
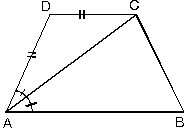
- Karşılıklı iki kenarı paralel olan dörtgenlerde açıortay verilmiş ise ikizkenar üçgen elde edebileceğimiz gibi, ikizkenarlık verilmiş ise de açıortay elde ederiz.
|
 |
2. Yamuğun Alanı
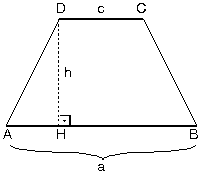
| ABCD yamuğunda paralelkenarlar arasındaki uzaklığayamuğun yüksekliği denir. Alt tabanı |DC| = a,üst tabanı |AB| = c
yüksekliği |AH| = h
ABCD yamuğunun alanı
|
 |
3. İkizkenar Yamuk
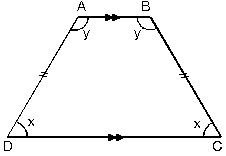
| Paralel olmayan kenarları eşit olan yamuklara ikizkenar yamuk denir. |
 |
| a. İkizkenar yamukta taban ve tepe açıları kendiaralarında eşittir.m(A) = m(B) = y
m(D) = m(C) = x
|
 |
| b. İkizkenar yamukta köşegen uzunlukları eşittir.Köşegenlerin kesiştiği noktaya E dersek|AE| = |EB|
|DE| = |CE|
|
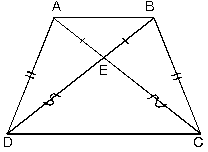 |
- Köşegen uzunlukları birbirine eşit olan her yamuk ikizkenardır.
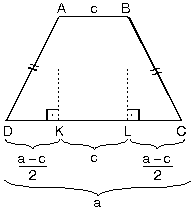
| c. İkizkenar yamukta üst köşelerden alt tabana diklerçizilmesiyle ADK ve BCL eş dik üçgenleri oluşur.|DC| = a|KL| = c
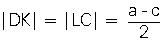
|
 |
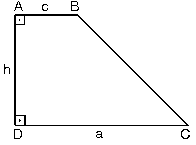
4. Dik Yamuk
| Kenarlarından biri alt ve üst tabana dik olan yamuğa dikyamuk denir.|AD| = h aynı zamanda yamuğun yüksekliğidir. |
 |
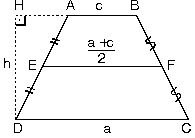
5. Yamukta Orta Taban
| a. ABCD yamuğunda E ve F kenarların orta noktaları ise EL doğrusuna orta taban denir.[AB] // [EF] // [DC]
|
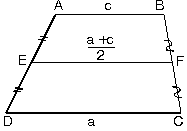 |
| A(ABCD)=Orta taban x Yükseklik |
b. Yamukta köşegenin orta tabanda ayırdığı parçalar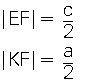 |
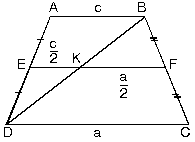 |
- ABCD yamuğunda EF orta taban
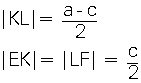
|
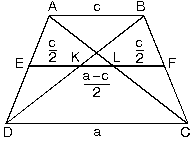 |
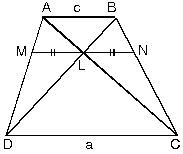
| 6. Yamuğun köşegenlerinin kesim noktasından tabanlaraçizilen paralel;ABCD yamuğunda L köşegenlerin kesim noktasıdır.
[AB] // [MN] // [DC]
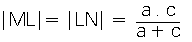
|
 |
7. Kenar Uzunlukları Bilenen Yamuk
| Bir ABCD yamuğunun kenar uzunlukları biliniyor ise kenarlardan birine paralel çizilerek bir paralelkenar ve bir üçgen oluşturulur. |
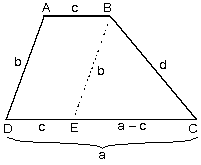 |
8. Köşegenleri Dik Kesişen Dik Yamuk
| ABCD dik yamuğunda[AC] ^ [BD] BD ye paralel çizildiğinde oluşan dik üçgende
|
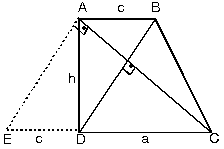 |
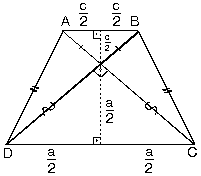
9. Köşegenleri Dik Kesişen İkizkenar Yamuk
| ABCD yamuğunda|AD| = |BC|
[AC] ^ [BD]
yamuğun yüksekliği
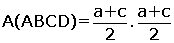
|
 |
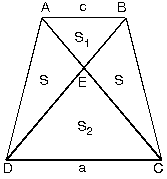
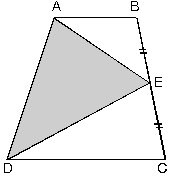
| Bir yamukta alt ve üst iki köşenin, karşı kenarın ortanoktası ile birleştirilmesi sonucu oluşan alan yamuğunalanının yarısına eşittir.
|BE| = |EC|
|
 |
| l [AB] // [EF] // [DC], |AB| = a|EF| = b
|DC| = c
A(ABFE) = S2
A(EFCD) = S1
|