YGS-LYS, Konu Anlatımı

Türev

Türev ,
Diğer sayı kümeleri üzerindeki fonksiyonlar için genellenmiş olmasına rağmen öncelikle reel değerli, yani reel sayılardan reel sayılara giden tek değişkenli fonksiyonlar için tanımlanmış, kabaca bir fonksiyonun grafiğine çizilen teğetin eğimini hesaplama tekniğidir. Bu türden bir f fonksiyonunun a noktasındaki türevin

Birinci tanımı(h türev)

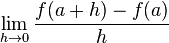
limiti olarak tanımlanır. Bu limitin temsil ettiği oran aşağıdaki grafikte gösterilmiştir.

Yukarıdaki grafikte h değeri sıfıra yaklaştıkça, d doğrusu da y=f(a) eğrisine (a,f(a)) noktasındaki teğete yaklaşır.

Burada :

ifadesinin de d doğrusunun eğimini verdiğine dikkat etmek gerekir.

Türevin birinci tanımını örnekleyerek bir ikinci tanım daha yapabiliriz.

ifadesinin mantığında {h}sonsuz küçüğünü ekleme işlem yapılmıştır,oysaki tanımı genelleştirebilmek mümkün;şöyleki sonsuz küçük artırımı yerine sonsuz küçük katının artırımıda yapılabilir.

İkinci tanımı(q türev)

Bir f(x) fonksiyonunu q türevi

sıklıkla Dqf(x) şeklinde yazılır, q-türev Jacksen türevi olarak bilinir.

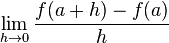ayrıca;

elde edilebilir.

Türev Alma

Türevlenebilir bir f fonksiyonu için her a noktasındaki değeri f fonksiyonun a noktasındaki türevi olan fonksiyona f fonksiyonun türevi denir ve bu fonksiyon f' sembolüyle gösterilir. Ayrıca

formülü de bu durumu ifade etmek için kullanılır.

Kesirli türev alma

fonksiyon f(x) = x(mavi eğri) için yarı türev (mor eğri) ve birinci türev (kırmızı eğri).

f(x) tek terimli varsayalım

Burada kullanılan türev

tekrarlana türev şu sonucu verir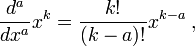

faktöriyel yerine Gama fonksiyonu'nu alalım

x'in yarı türevi

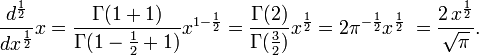
Bu durumu tekrarlarsak

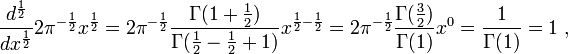Gerçekten burada beklenen sonuç aynıdır.

Burdaki türev alma işlemi sadece gerçel sayılarla sınırlı değildir örneğin, (1+i)inci türev , (1-i)inci türev iki türevlidir. ancak negatif değerler için alınan a integrali verir.

Kısmi Türev

Kısmi türevçok değişkenli bir işlevin, sadece ilgili değişkeni sabit değilken alınan türevdir. Bu tarz türevleri içeren denklemlere kısmi diferansiyel denklem denir.

Tanım

z = f(x1,x2,...,xm,...,xn)
biciminde tanimlanan n tane bagimsiz deg*****e bagli surekli z fonksiyonunun diğer değişkenler sabit tutularak herhangi bir değişkendeki Δxm degisimine karşılık fonksiyonun değişim hızı

Δxm = h

ifadesine z fonksiyonunun xm değişkenine göre kısmi türevi denir.

şeklinde gösterilir.

ise;

Örnek:

Türevlenebilir Fonksiyonlar ve Türevleri

Herhangi bir sıfırdan farklı n reel sayısı için f(x) = xn fonksiyonu,

Bu eşitlik Binom Teoremi'nin bir sonucudur. (Bu formul yalnızca reel sayilarda kullanılır ! )

sin(x) ve cos(x) trigonometrik fonksiyonları,

ex fonksiyonu,

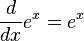
Türevlenebilir Olmayan Fonksiyonlar

Mutlak değer fonksiyonu 0 noktasında türevli değildir. Nedeni, 0'da türevi tanımlayan

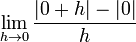limitinin bulunamamasıdır. Diğer her noktada türevlidir.

fonksiyonu da 0'da türevli olmayıp da başka her yerde türevli olan bir fonksiyondur. Bu fonksiyonun 0'da türevlenebilir olmayışının nedeni

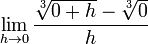limitinin

, yani sonsuz olmasıdır. Dolayısıyla mutlak değer fonksiyonunun grafiği 0 noktasında kırıkken,

fonksiyonunun grafiği 0'da da kırılmasızdır.
Temel Teoremler

Çok karmaşık görünümlü fonksiyonların da türevlerini almamızı kolaylaştıracak teknikler (teoremler) mevcuttur.

(f + g)'(a) = f'(a)+ g'(cf)'(a) = cf'(a),

(fg)'(a) = f'(a)g(a) + g'(a)f(a) (Çarpım Kuralı olarak bilinir),

(f o g)'(a) = f'(g(a)) x g'(a) (Zincir kuralı olarak bilinir).

(f/g)'(a) = [f'(a)g(a) - g'(a)f(a)]/g²(a) (Fark Kuralı),

Daha fazla bilgi için Türev alma kuralları maddesine bakınız.
Genellemeler

Türev alma operasyonunu birden çok kez uygulamak mümkündür. Eğer f' , f fonksiyonunun türeviyse ve de f", f' fonksiyonunun türeviyse o zaman f" fonksiyonuna f fonksiyonunun ikinci türevi denir. Daha yüksek dereceden türevler de benzer şekilde tanımlanır.

Türevi alınan f fonksiyonunun reel değerli olması şart değildir. Mesela f Karmaşık Sayılar veya p-sel Sayılar üzerinde tanımlı bir fonksiyon olabileceği gibi aldığı değerleri de reel sayılar dışındaki uygun bir kümeden (mesela gene karmaşık sayılar kümesi olabilir) alıyor olabilir.

Tek değişkenli olmayan fonksiyonların da türevlerinden bahsetmek mümkündür, ancak önce yukardaki limitli tanımı ve teğet doğrusu argümanını bu duruma uyarlamak gereklidir. Bu konu Kısmi Türev makalesinde bulunabilir.

Türevin uygulamaları

f fonksiyonunun a noktasında türevi, f'nin grafiğine a noktasında çizilen teğetin eğimini verdiğinden bir fonksiyonun birinci ve ikinci türevlerine bakarak o fonksiyonun grafiğinin davranışları hakkında grafiği kaba taslak çizmemize yetecek kadar bilgi edinmemiz mümkündür.

Hesabın temel teoremi'ne göre türev almakla integral almak, birbirlerinin tersi olan iki operasyondur.

Taylor açılımları, bir fonksiyonun bir noktadaki ilk birkaç dereceden türevini kullanarak o fonksiyona yakın bir polinom ifadeli fonksiyon bulmamıza yararlar. Çoğu zaman polinom ifadeli olmayan bir fonksiyonun bir noktadaki tam değerini bulmak sonsuz sayıda işlem gerektirdiğinden buna karşılık polinom değerli fonksiyonların deşerini hesaplamak sonlu bir işlem olduğundan bu açılımlar ve türev kavramı vazgeçilmezdir.

Yaygın doğa felsefesi görüşüne göre, doğada gerçekleşen fiziksel olayların tümü sürekli yumşak geçişlidir. Tıpkı buzluktan çıkardığımız bir buzun aniden değil de yavaş yavaş erimesinde olduğu gibi. Dolayısıyla fiziksel olayları tarif etmekte kullanılan fonksiyonların hemen hepsinin türevlenebilir olması beklenir. Matematiğin diferansiyel denklemler dalı, doğada gözlenen verilerden bu tür fonksiyonlar çıkartma yöntemleri bulmak amacıyla geliştirilmiştir.

Matematiğin diferansiyel geometri ve diferansiyel topoloji alanları öncelikle türevlenebilir fonksiyonlar aracılığıyla tarif edilebilen geometrik yapılarla ilgilenirler.

Çarpım ve Bölüm Fonksiyonlarının Türevi